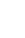Pienet lapset ovat luonnostaan innokkaita omaksumaan uusia asioita. Useimmat heistä hinkuvat oppia lukemaan ja laskemaan. Kannustaminen ja oppimaan innostaminen on suurimmalle osalle vanhemmista luonnollista. Tämä on tärkeää ja hienoa, jotain jota jokaisen kasvattajan tulisi tehdä! Meidän tulee kuitenkin ottaa huomioon, että saatamme joskus myös vahingossa kylvää väärinkäsityksen siemenen, pahaa tarkoittamatta.
Vanhemmat kertovat usein ylpeinä lastensa saavutuksista: “Meidän Liisa osaa laskea jo sujuvasti 10:een”
Ehkä hän osaa laskea jopa sataan saakka?
Pienten lasten lukukäsitteen ymmärtämisessä voi kuitenkin olla suuria ongelmia ja eroja. Tämä tulee esille lukumäärän ja sen symbolin välisessä ymmärryksessä. Vaikka lapsi osaisi luetella luvut 10:een saakka, se ei takaa, että hän ymmärtäisi ne lukumäärinä. Useat lapset onnistuvat ratkaisemaan yksinkertaisia laskuja, mutta ovat usein oppineet muistamaan nämä vastaukset ulkoa tai laskevat niitä vielä sormien avulla. Edellä kuvattu toimintamalli perustuu pinnalliseen ymmärrykseen luvuista, eikä poraudu niihin syvemmälle.

Lukukäsite on intuitiivinen ymmärrys miten luvut muodostuvat ja miten niitä voidaan manipuloida matemaattisten operaatioiden kautta. Jotta lapselle muodostuu oikeanlainen ja vahva mentaalimalli, hänen tulisi ymmärtää miten luvut toimivat, mistä ne muodostuvat ja mitä ne edustavat. Vahva perusta myöhemmälle matemaattiselle oppimiselle luodaan, kun lapsi onnistuu kehittämään syvällisen ymmärryksen lukujen ympärillä. Hänellä on tällöin mahdollisuus käyttää monipuolisia ja erilaisia laskustrategioita.
1. Lukumäärän hahmottaminen
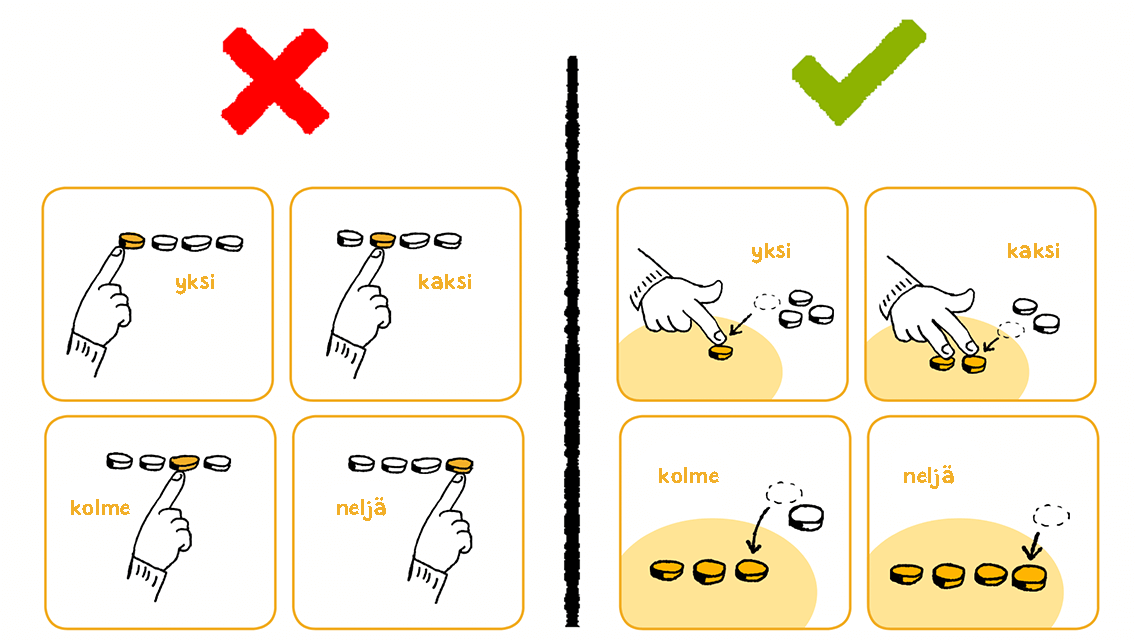
Yksinkertaisesti: muuta tapaa jolla lasket. Sen sijaan, että lasket yksittäisiä asioita tai esineitä näyttämällä niiden paikkaa lukusuoralla sormella osoittaen, on oleellista oppia ymmärtämään luvut niitä edustavina lukumäärinä. Tämä saadaan aikaiseksi, kun muodostat lukua edustavan määrän laskemisen yhteydessä. Lapsen sanoessa lukua ääneen, hänen tulisi osoittaa koko lukumäärää tarkoittavaa havaintoa, eikä vain sen paikkaa lukusuoralla:
2. Lukumäärän tunnistaminen
Varhaisessa vaiheessa, lukukäsitteen kehittymisen kannalta, on oleellista oppia tunnistamaan pieniä määriä ilman erillistä laskemista. Ensimmäinen askel on pystyä erottamaan yksi esine kahdesta, ilman että niitä tarvitsee konkreettisesti erikseen laskea. Määrien nimeäminen “yhdeksi” ja “kahdeksi” on tärkeää. Seuraava askel on esitellä luku kolme ja harjoitella tunnistamaan kolmen ryhmiä ilman erillistä laskuprosessia. Jos lapsi onnistuu tässä, olet luonut hyvän pohjan matemaattisen ymmärryksen kehittymiselle.
3. Lukujen ymmärrys ryhmittelyn avulla
Kun me aikuiset tunnistamme viiden lukumäärän koostuvan viidestä objektista, johtuu se siitä, että ryhmittelemme sen automaattisesti mielessämme. Ymmärrämme, että määrä voi koostua esim. kolmen ja kahden objektin kokonaisuudesta. Tämän rinnalla tiedämme, että 2 ja 3 tekee yhteensä 5. Tämä automaatio puuttuu lapsilta, joilla on vaikeuksia käsittää lukumääriä.
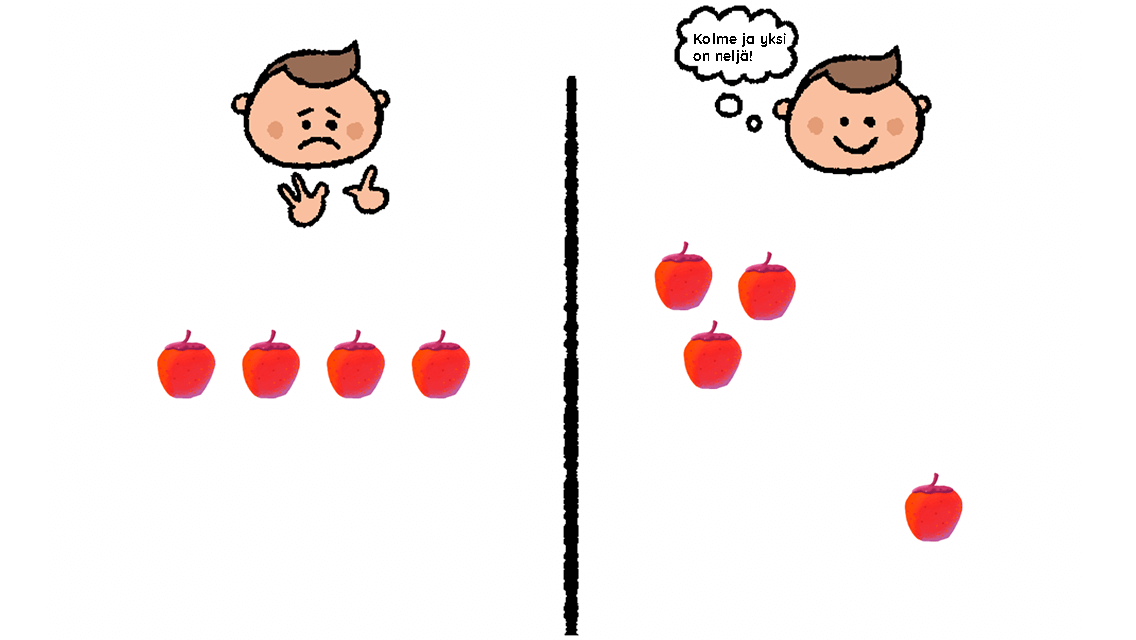
Sen vuoksi on tärkeää esitellä nelonen “yhden suurempana kuin kolme”. Kun lapsi näkee neljä objektia, voi ryhmittelyä harjoitella kolmen ja yhden kautta, jolloin saadaan aikaan nelonen. Osa lapsista ymmärtää tämän omatoimisesti, kun taas osa lapsista tarvitsee monta toistokertaa vuosien ajan automaation juurruttamiseen.
4. Laskeminen ryhmittelyn avulla
Kaikki luvut voidaan esitellä lapsella “yhden suurempana kuin” -menetelmällä. Oppimisen seuraava vaihe on tämän jälkeen opetella lukujen hajotelmia selittämällä: luku viisi voidaan saada aikaiseksi nelosen ja ykkösen sekä kolmosen ja kakkosen avulla. Tämä pätee myös viittä suurempiin lukuihin, ja on erinomainen tapa esitellä lapselle “viiden malli”: kuusi on 5 ja 1, seitsemän on 5 ja 2, kahdeksan on 5 ja 3, yhdeksän on 5 ja 4, kymmenen on 5 ja 5.

Jos lapsi onnistuu ymmärtämään tämän, on hänelle kehittynyt hyvä mentaalimalli luvuista. Tämä mahdollistaa lapselle joustavan ja monipuolisen tavan käsitellä lukuja ja laskemista. Täydellinen pohja tulevaisuuden hyvälle matemaattiselle oppimiselle luodaan, kun lapsi kokee oppimisen iloa matematiikan ympärillä, ymmärtäessään lukujen muodostamisen ja hajottamisen.